Les fonctions numériques servent à modéliser des phénomènes continus périodiques comme des signaux électriques ou pour étudier des ondes sonores.
Cercle trigonométrique
Définitions
On peut "enrouler" l'axe des réels autour d'un cercle de rayon 1, comme l'illustre l'animation ci-dessous :
-
Déplacer les deux curseurs
Enroulementet ceuxProfondeur de la graduationafin de visualiser l'enroulement de certains nombres réels particuliers sur le cercle trigonométrique. -
Entre les fractions décimales et celles avec $\pi$, lesquelles se placent à des endroits remarquables du cercle trigonométrique ?
-
Entre les fractions décimales et celles avec $\pi$, lesquelles se superposent précisément au bout d'un tour d'enroulement sur le cercle trigonométrique ?
-
On appelle cercle trigonométrique $\mathcal{C}$ dans le plan muni du repère orthonormal $(O ; \overrightarrow{i}, \overrightarrow{j})$ le cercle de centre $O$, de rayon $1$, pour lequel on choisit pour sens direct le sens inverse des aiguilles d’une montre.
-
À tout nombre réel $x$, on associe le point unique $M$ du cercle $\mathcal{C}$ tel qu’une mesure, en radians, de l’angle orienté $(\overrightarrow{i},\overrightarrow{OM})$ soit $x$.
-
Soit $x$ un réel et soit $M$ le point de $\mathcal{C}$ tel que $(\overrightarrow{i},\overrightarrow{OM})=x$.
Le point $M$ a pour abscisse $\cos(x)$ et pour ordonnée $\sin(x)$.
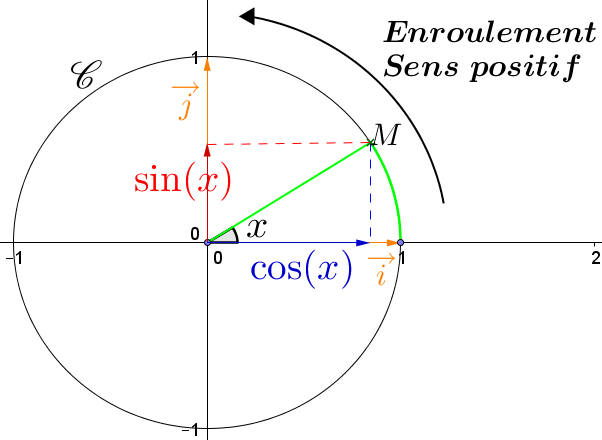
Comme un tour complet du cercle trigonométrique correspond à un angle de $2\pi$ (radians), si une mesure de $(\overrightarrow{i},\overrightarrow{OM})$ est $x$ alors les autres mesures sont : $x+k 2\pi$ avec $k$ un entier naturel relatif (c'est-à-dire $k\in\mathbb{Z}$).
Pour tout réel $t$ :
-
$-1\le \cos(t) \le 1$.
-
$-1\le \sin(t) \le 1$.
-
$(\cos(t))^2+(\sin(x))^2 = 1$.
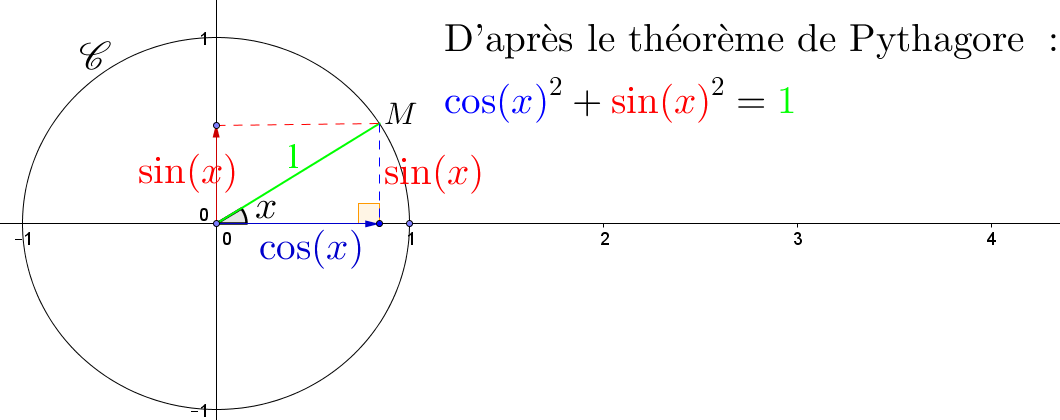
Valeurs à connaître
En utilisant la relation $(\cos(t))^2+(\sin(t))^2 = 1$, on peut démontrer les valeurs suivantes :
| $t$ | $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ |
|---|---|---|---|---|---|
| $\sin(t)$ | $0$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $1$ |
| $\cos(t)$ | $1$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ |
À partir de ces valeurs, on peut déduire l'ensemble des valeurs remarquables à connaître au lycée sur le cercle trigonométrique :
Cercle complet à connaître par cœur :
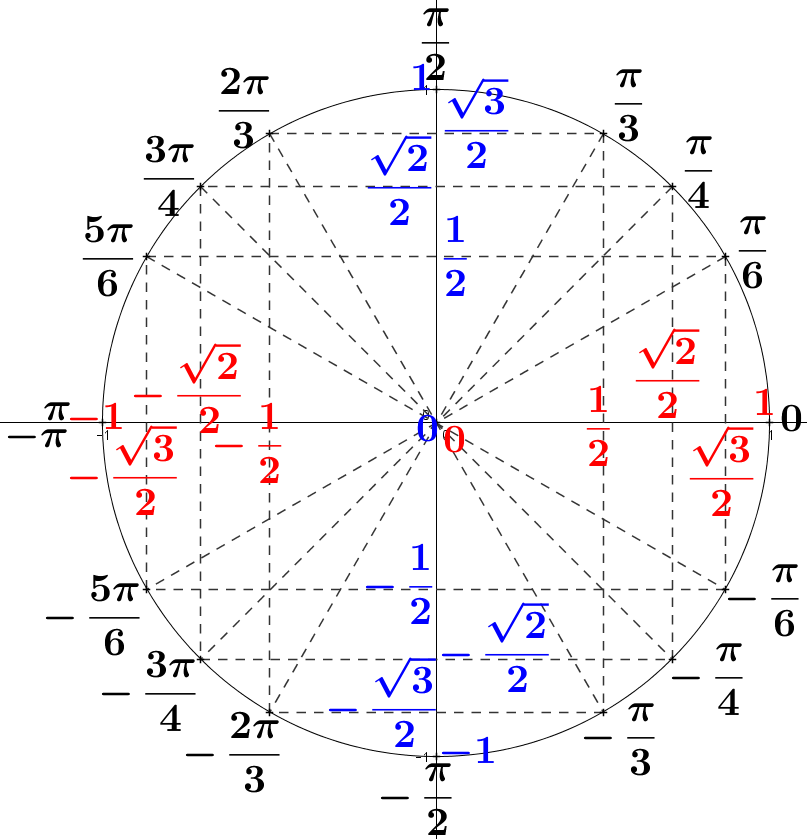
De mémoire, construire le cercle trigonométrique complet précis sur l'intervalle $[-\pi;\pi]$ où apparaissent à la fois les angles remarquables $x$ et les valeurs correspondantes $\cos(x)$ et $\sin(x)$.
Voici un test portant sur le placement des angles remarquables de $[-\pi;\pi]$ sur le cercle trigonométrique.
Voici un test portant sur la connaissance des valeurs associées à des angles remarquables sur $[-\pi;\pi]$.
Utiliser le cercle trigonométrique afin de résoudre les équations suivantes sur $[-\pi ;\pi]$ :
-
$\sin(x)=\dfrac{1}{2}$
-
$\cos(x)=-\dfrac{\sqrt{3}}{2}$
-
$\cos(x)=\dfrac{\sqrt{2}}{2}$
-
$(2\sin(x)+1)(\sqrt{3}-2\cos(x))=0$
-
$(\cos(x)+1)\cos(x)\sin(x)=0$
Une scène de concert comporte un arc permettant de placer des projecteurs à différents points de cet arc.
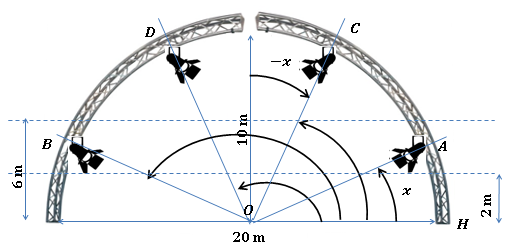
Le projecteur A se trouve à la position formant un angle de $\dfrac{\pi}{6}$ par rapport à l’horizontale.
À quelle hauteur se situent les projecteurs A et C dans la scène ?
Voici un test portant sur la résolution d'équations trigonométriques dans $[-\pi;\pi]$.
Utilisation de Xcas
-
La fonction sinus est saisie sur Xcas comme
sin(t). -
La fonction cosinus est saisie sur Xcas comme
cos(t).
Résoudre sur Xcas l'équation $(\cos(x))^2=1$ sur l'intervalle $[-\pi;\pi]$.
-
Essayer de résoudre sur Xcas l'inéquation $\cos(x)>0$ sur l'intervalle $[-\pi;\pi]$.
Quel problème rencontrez-vous ? -
Rajouter l'instruction
supposons(x>=-pi and x<=pi).
Relancer le code pour résoudre l'inéquation $\cos(x)>0$ sur l'intervalle $[-\pi;\pi]$. -
Rajouter l'instruction
purge(x)afin de supprimer la condition imposée surxpour ne pas polluer d'autres calculs demandés.
Pour résoudre une inéquation sur Xcas, il suffit :
-
commencer par définir l'ensemble des valeurs où l'on cherche des solutions à l'aide de l'instruction
supposons(ou son équivalent anglaisassume), -
utiliser l'instruction
solve(inequation,inconnue).
Résoudre dans $[-\pi;\pi]$ l'inéquation $\sin(x)<\dfrac{1}{2}$.
Courbes représentatives
Le but est de découvrir la courbe représentative des fonctions $\sin$ et $\cos$.
-
Dans le fichier GeoGebra intégré ci-dessous, déplacez le curseur en dessous de "Angle : " du graphique de gauche.
-
Dans le fichier GeoGebra intégré ci-dessus, cochez la puce "trace points" dans le graphique de droite, puis déplacer le curseur "Angle" pour visualiser un ensemble de points appartenant aux courbes représentatives.
-
Cochez la puce "fonction cosinus" pour faire apparaître la courbe représentative de la fonction $\cos$.
-
Cochez la puce "fonction sinus" pour faire apparaître la courbe représentative de la fonction $\sin$.
Voici la courbe représentative des fonctions $\sin$ et $\cos$ :
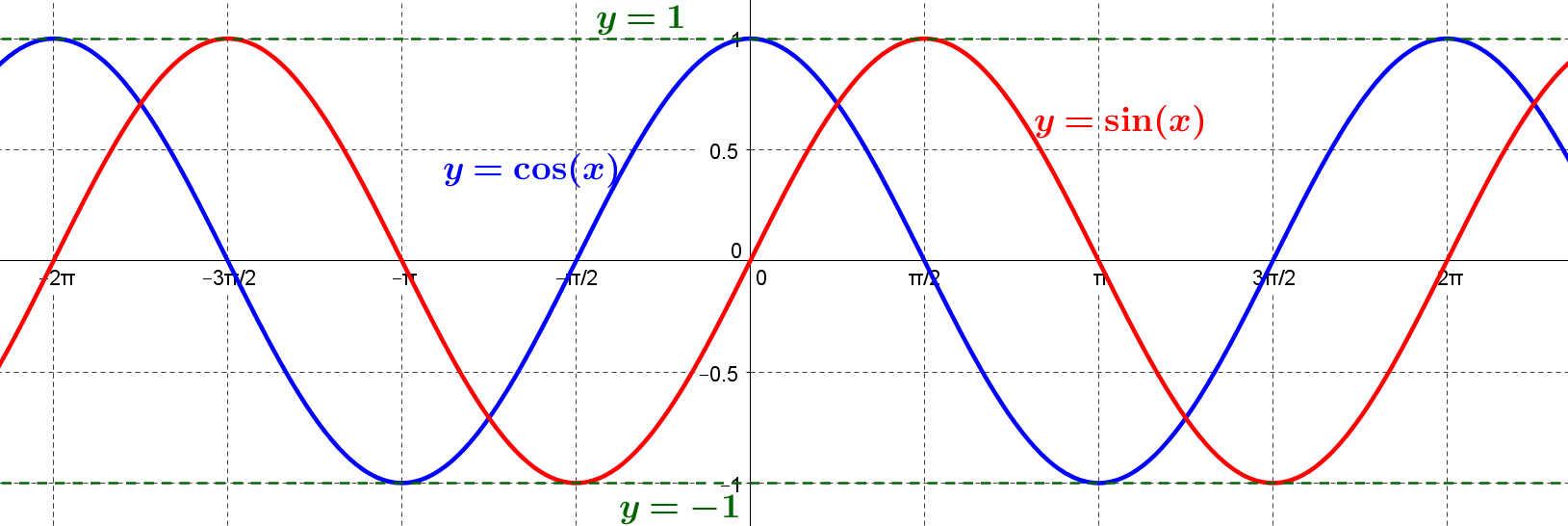
Parité et périodicité
Définitions
Le but est de découvrir la notion de parité d'une fonction.
-
Dans le fichier GeoGebra intégré ci-dessous, déplacez le curseur en dessous de "Exposant : ".
-
Quelle symétrie est commune à toutes les courbes en bleu représentant les fonctions $x\mapsto x^n$ lorsque l'exposant $n$ est pair ?
-
Quelle symétrie est commune à toutes les courbes en rouge représentant les fonctions $x\mapsto x^n$ lorsque l'exposant $n$ est impair ?
-
Cochez la puce "paire" pour vérifier la symétrie conjecturée précédemment en déplaçant le curseur nommé "abscisse".
-
Cochez la puce "impaire" pour vérifier la symétrie conjecturée précédemment en déplaçant le curseur nommé "abscisse".
Dire qu’une fonction $f$ définie sur $\mathbb{R}$ est paire signifie que pour tout réel $t$ : $f(-t)=f(t)$.
Si une fonction $f$ est paire, alors sa courbe représentative est symétrique par rapport à l'axe des ordonnées.
La fonction carré et plus généralement toutes les fonctions $t\mapsto t^{n}$, avec $n$ pair, sont des fonctions paires.
Dire qu’une fonction $f$ définie sur $\mathbb{R}$ est impaire signifie que pour tout réel $t$ : $f(-t)=-f(t)$.
Si une fonction $f$ est impaire, alors sa courbe représentative est symétrique par rapport à l'origine.
La fonction cube et plus généralement toutes les fonctions $t\mapsto t^{n}$, avec $n$ impair, sont des fonctions impaires.
Regarder les courbes représentant respectivement les fonctions $\cos$ et $\sin$.
Quelle parité peut-on conjecturer pour chacune de ces deux fonctions ?
-
La fonction $\sin$ est impaire : pour tout réel $t$, on a : $\sin(-t)=-\sin(t)$.
-
La fonction $\cos$ est paire : pour tout réel $t$, on a : $\cos(-t)=\cos(t)$.
Chaque saison revient périodiquement chaque année. Cela signifie que rajouter 1 (an) au temps $t$ ne change rien à la saison.
On peut généraliser cette idée à des fonctions mathématiques :
Soit $T$ un nombre réel positif non nul.
Dire qu’une fonction $f$ définie sur $\mathbb{R}$ est périodique de période $T$ ou
$T$-périodique signifie que pour tout réel $t$, on a : $f(t+T)=f(t)$.
Cette fonction tracée est périodique de période 2 (on dit aussi 2-périodique) :
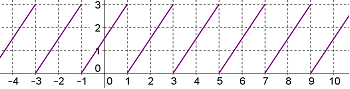
-
Regarder les courbes représentant respectivement les fonctions $\cos$ et $\sin$.
Pourquoi peut-on conjecturer que les fonctions $\sin$ et $\cos$ sont périodique ? -
Quelle période peut-on conjecturer pour chacune de ces deux fonctions ?
Les fonctions $\sin$ et $\cos$ sont périodiques de période $2\pi$.
La courbe d'une fonction périodique se construit par le décalage répété d'un "motif" : la courbe réduite à un intervalle de longueur la période de cette fonction.
Ci-dessous le motif représentant la fonction $\sin$ sur l'intervalle $[-\pi;\pi]$ se superpose à la courbe
représentant la fonction $\sin$ sur $[\pi;3\pi]$ par décalage (=translation) de
vecteur $2\pi \overrightarrow{i}$ :

Utilisation pour le tracé de courbe
La connaissance de la parité ou de la périodicité d'une fonction définie sur $\mathbb{R}$ permet de réduire l'intervalle sur lequel il suffit d'étudier la fonction :
-
Pour étudier une fonction paire ou impaire, il suffit de travailler sur $[0 ; +\infty[$, les résultats sur l’autre partie se déduisant par symétrie.
-
Pour étudier une fonction périodique, il suffit de travailler sur un intervalle de longueur $T$. Les résultats sur le reste du domaine s’en déduisent par translation de vecteur $T\overrightarrow{i}$.
Comment représenter sur l'intervalle $[-9;9]$ la fonction impaire et périodique de période 6 définie par :
$f(t)=2t$ sur $[0;1]$ et $f(t)=3-t$ sur $[1;3]$ ?
La vidéo ci-dessous explicite la démarche :
Vous pouvez retrouver les étapes de construction présentées dans la vidéo en cliquant sur le bouton
 en bas du
graphique Geogebra imbriqué ci-dessous :
en bas du
graphique Geogebra imbriqué ci-dessous :
Tracer la représentation graphique sur l'intervalle $[-8;8]$ de la fonction $f$, paire et périodique de période 4, définie sur l'intervalle $[0;1]$ par $f(t)=2-t$ et sur l'intervalle $[1;2]$ par $f(t)=1$.
Vous pouvez vous aider de la vidéo de l'exemple précédent.
Soit le signal $s$ défini sur $[0;5]$ par la courbe représentative suivante :

Reproduire sur une feuille la courbe précédente et la prolonger de sorte que le signal ainsi représenté soit impair et périodique de période 10.
Soit le signal $s$ défini sur $[0;4]$ par la courbe représentative suivante :
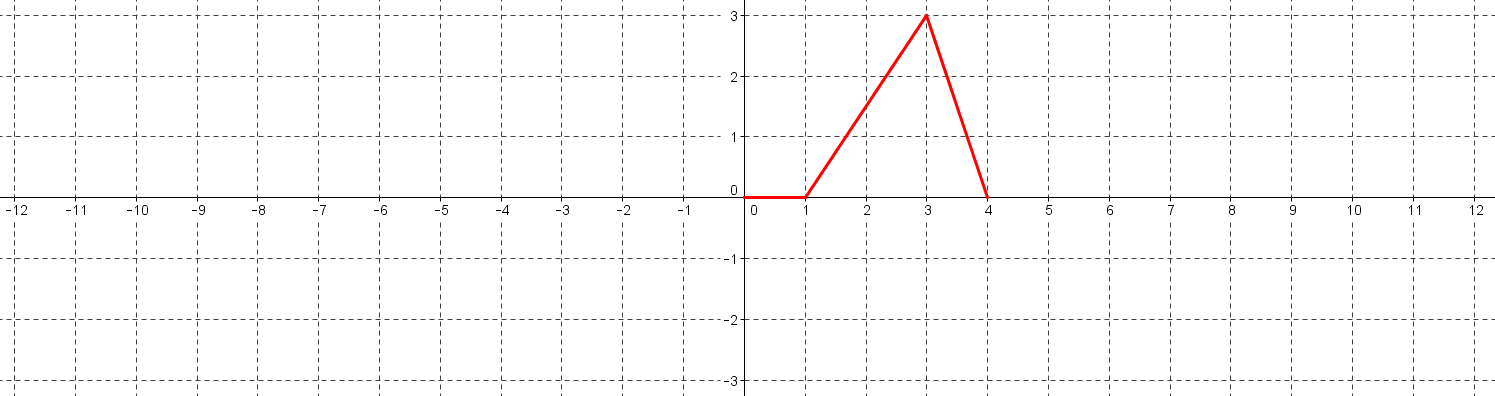
-
Reproduire et prolonger sur [-12;12] la courbe représentative ci-dessus de sorte que le signal ainsi représenté soit périodique de période 4 et prolonge le signal $s$.
-
Le signal ainsi prolongé est-il pair ? Justifier.
-
Le signal ainsi prolongé est-il impair ? Justifier.
Soit le signal $s$ défini sur $[0;3]$ par la courbe représentative suivante :
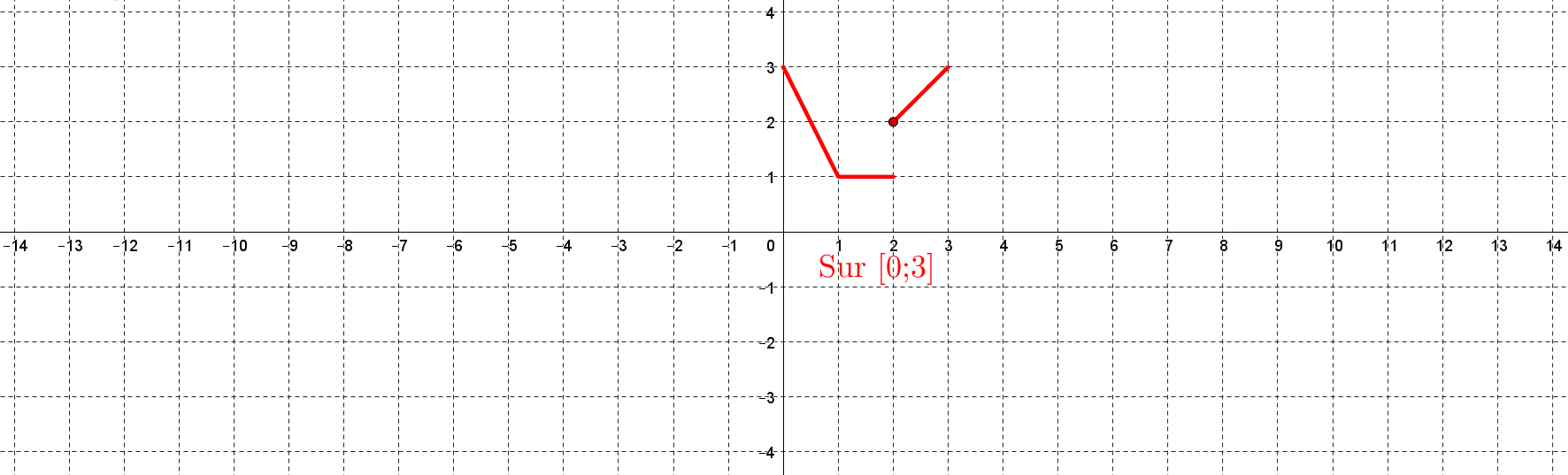
Reproduire sur une feuille la courbe précédente et la prolonger de sorte que le signal ainsi représenté soit pair et périodique de période 6.
Le point marqué en $(2;2)$ signifie que le signal $s$ est tel que $s(2)=2$ ; le point de coordonnées $(2;1)$ n'appartient pas à la courbe représentant le signal $s$.
Fonction tangente
La fonction tangente est définie pour tout réel $t$ tel que $t\neq \dfrac{\pi}{2}+k\pi$ avec $k$ un entier relatif, par $\tan(t)=\dfrac{\sin(t)}{\cos(t)}$.
La condition $t\neq \dfrac{\pi}{2}+k\pi$ signifie que $\cos(t)$ doit être non nul pour ne pas diviser par 0.
Voici les valeurs particulières obtenues à partir des valeurs particulières de $\sin(t)$ et de $\cos(t)$ :
| $t$ | $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ |
|---|---|---|---|---|---|
| $\tan(t)$ | $0$ | $\dfrac{\sqrt{3}}{3}$ | $1$ | $\sqrt{3}$ |
N'existe pas ! |
Sur Geogebra et sur Xcas, cette fonction tangente est saisie avec tan(x).
-
Tracer la courbe représentative de la fonction tangente sur GeoGebra.
-
Comment voir que la fonction tangente n'est pas définie sur $\mathbb{R}$ mais qu'elle admet des valeurs interdites ?
Voici la courbe représentative de la fonction tangente (en noir) :
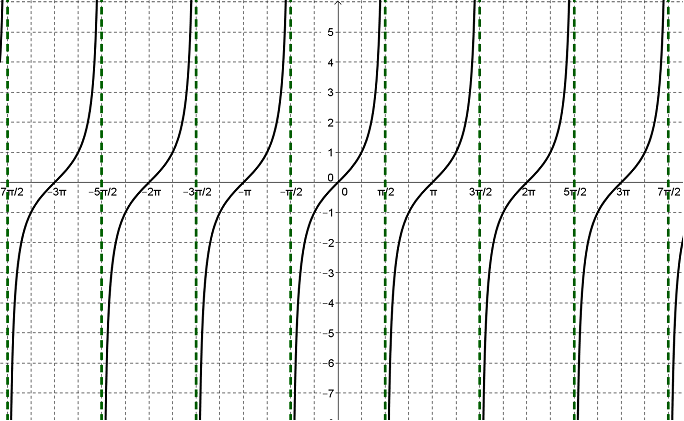
On retrouve sur cette courbe que la fonction tangente n'est pas définie lorsque $t=\dfrac{\pi}{2}+k\pi$ avec $k$ un entier relatif.
La courbe se rapproche alors des droites verticales (en pointillés verts) sans jamais les "toucher" ; ces droites sont appelées des
asymptotes à la courbe représentant la fonction tangente.
En étudiant la courbe représentative de la fonction tangente, déterminer :
-
Si la fonction tangente est périodique et si oui, quelle est sa période.
-
La parité éventuelle de la fonction tangente.
-
La fonction tangente est périodique de période $\pi$ :
Pour tout $t\neq \dfrac{\pi}{2}+k\pi$ avec $k$ un entier relatif, $\tan(t+\pi)=\tan(t)$. -
La fonction tangente est impaire :
Pour tout $t\neq \dfrac{\pi}{2}+k\pi$ avec $k$ un entier relatif, $\tan(-t)=-\tan(t)$.
Dérivées des fonctions trigonométriques
-
$(\sin(t)')=\cos(t)$.
-
$(\cos(t)')=-\sin(t)$.
-
$(\tan(t)')=\dfrac{1}{(\cos(t))^2}$.
La dérivée précédente peut aussi être écrite sous la forme : $(\tan(t)')=1+(\tan(t))^2$.
Soit $u$ est une fonction dérivable sur $\mathbb{R}$ telle que les fonctions ci-dessous existent.
-
$(\sin(u))'=u'\times \cos(u)$.
-
$(\cos(u))'=-u'\times \sin(u)$.
-
$(\tan(u))'=\dfrac{u'}{(\cos(u))^2}$.
-
$(\tan(u))'=u'\times\left(1+(\tan(u))^2\right)$.
-
Pour tout réels $\omega$ et $\phi$, on a : $(\sin(\omega t + \phi))'=\omega\times \cos(\omega t + \phi)$.
-
Pour tout réels $\omega$ et $\phi$, on a : $(\cos(\omega t + \phi))'=-\omega\times \sin(\omega t + \phi)$.
Utiles pour la physique :
Sur Xcas, vous pouvez utiliser l'instruction deriver(fonction,variable) pour obtenir une expression
de la dérivée de la fonction saisie.
-
Un signal électrique est donné par $s:t\mapsto 220\sin(100\pi t)$.
Dériver à la main $s$ sur $\mathbb{R}$. -
Vérifier la dérivée obtenue sur Xcas.
Le but est d'étudier les variations de la fonction $f$ définie sur $[-\pi;\pi]$ par : $f(t)=\dfrac{1}{3}(\sin(t))^3+\dfrac{1}{2}(\sin(t))^2$.
Pour cela, vous avez déjà obtenu sur Xcas l'ensemble des résultats suivant :

-
Quel(s) code(s) permet(tent) à Xcas de pouvoir résoudre l'inéquation $\sin(x)>0$ sur $[-\pi;\pi]$ ?
-
Quel est le rôle de l'instruction
purge(x)(à la ligne 10) ? -
Dresser le tableau de variations complet pour $f$ sur $[-\pi;\pi]$ :
Quatre villes sont situées aux quatre sommets d'un carré de côté 100 km.
On se propose de les relier par un réseau d'autoroutes de longueur minimale.
A, B, C et D sont les quatre sommets du carré. E et F sont les points de jonction des autoroutes.
On désigne par $\alpha$ une mesure en radians de l'angle $\widehat{ABE}$ et par $f(\alpha)$ la longueur totale du réseau.
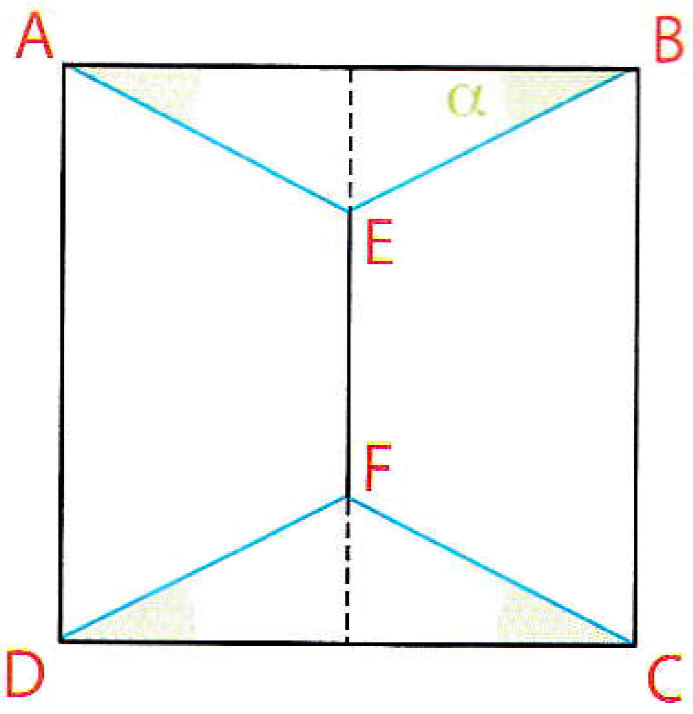
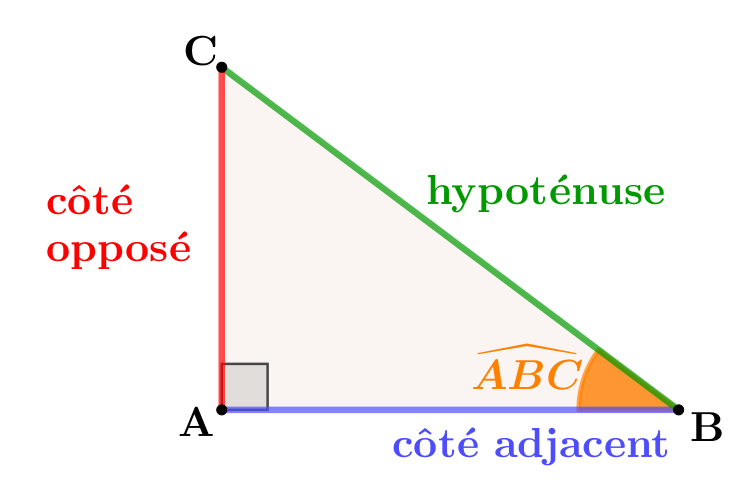
On rappelle les formules de trigonométrie que l'on peut utiliser dans tout triangle rectangle $ABC$, rectangle en $A$ :
-
$\cos(\color{orange}{\widehat{ABC}})=\dfrac{\color{#0000FF}{\text{côté adjacent}}}{\color{#009900}{\text{hypoténuse}}}=\dfrac{\color{#0000FF}{AB}}{\color{#009900}{BC}}$.
-
$\sin(\color{orange}{\widehat{ABC}})=\dfrac{\color{#FF0000}{\text{côté opposé}}}{\color{#009900}{\text{hypoténuse}}}$ $=\dfrac{\color{#FF0000}{AC}}{\color{#009900}{BC}}$.
-
$\tan(\color{orange}{\widehat{ABC}})=\dfrac{\color{#FF0000}{\text{côté opposé}}}{\color{#0000FF}{\text{côté adjacent}}}$ $=\dfrac{\color{#FF0000}{AC}}{\color{#0000FF}{AB}}$.
-
Justifier que $EF=100-100\tan(\alpha)$.
-
En déduire que $f(\alpha)=100+\dfrac{200}{\cos(\alpha)}-100\tan(\alpha)$, avec $0\le \alpha \le \dfrac{\pi}{4}$.
-
Dresser le tableau de variations de $f$ sur $\left[0;\dfrac{\pi}{4}\right]$.
-
En déduire la longueur totale minimale du réseau et la valeur de $\alpha$ qui permet d'obtenir ce minimum.
Fonction arctangente
Définition
La fonction $f=\tan$ est dérivable et strictement croissante sur l'intervalle $\left]-\dfrac{\pi}{2};\dfrac{\pi}{2}\right[$ à
valeurs dans l'intervalle $]-\infty;+\infty[$ car alors $f'(t)=\dfrac{1}{(\cos(t))^2} >0$.
On obtient le tableau de variations suivant :
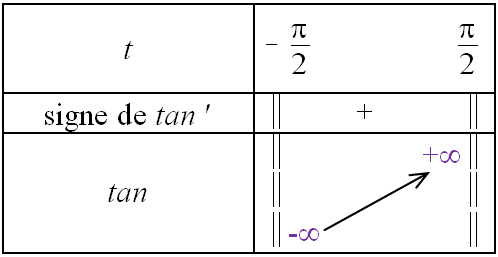
Pour chaque réel $y$, il existe un unique réel $t$ tel que $\tan(t)=y$.
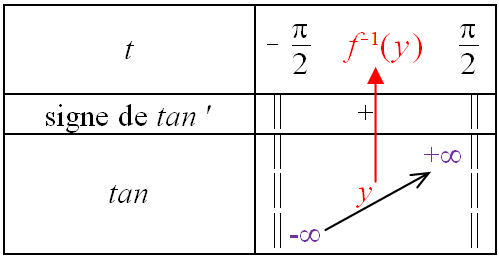
La fonction tangente $f$ admet donc sur une fonction réciproque, notée $f^{-1}$, définie sur $]-\infty;+\infty[$ par $f^{-1}(y)=t$ avec $t$ tel que $\tan(t)=y$.
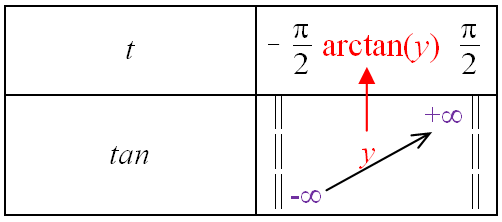
La fonction réciproque de la fonction tangente est appelée la fonction arctangente et on la note
$\arctan:y\mapsto \arctan(y)$.
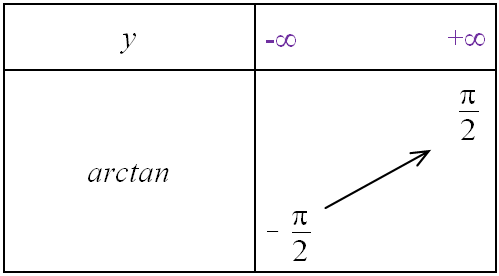
La fonction $\arctan$ est strictement croissante sur $]-\infty;+\infty[$
à valeurs dans l'intervalle $\left]-\dfrac{\pi}{2};\dfrac{\pi}{2}\right[$.
-
$0=\color{blue}{\tan}(0)$ donc $\color{red}{\arctan}(0)=0$.
-
$1=\color{blue}{\tan}\left(\dfrac{\pi}{4}\right)$ donc $\color{red}{\arctan}(1)=\dfrac{\pi}{4}$.
-
$\sqrt{3}=\color{blue}{\tan}\left(\dfrac{\pi}{3}\right)$ donc $\color{red}{\arctan}(\sqrt{3})=\dfrac{\pi}{3}$.
-
$\dfrac{\sqrt{3}}{3}=\color{blue}{\tan}\left(\dfrac{\pi}{6}\right)$ donc $\color{red}{\arctan}\left(\dfrac{\sqrt{3}}{3}\right)=\dfrac{\pi}{6}$.
Lors de l'étude d'un choc de marteau sur une enclume munie d'un système d'amortisseurs, on est amené à considérer la fonction $f$ définie sur $[0;+\infty[$ par $f(t)=\dfrac{507}{10}\cos(5\pi t)-\dfrac{13}{5}\sin(5\pi t)$, où $t$ correspond au temps mesuré en secondes.
-
-
Montrer que pour tout réel positif $t$, $f\left(t+\dfrac{2}{5}\right)=f(t)$.
-
En déduire que $f$ est périodique d'une période $T$ à détailler et expliquer comment interpréter concrètement cette périodicité au niveau du marteau.
-
-
Montrer que résoudre l'équation $f(t)=0$ revient à résoudre l'équation $\tan(5\pi t)=\dfrac{39}{2}$.
-
Montrer que si $T$ est une solution de l'équation $f(t)=0$, alors $T+\dfrac{1}{5}$ est aussi une solution de l'équation $f(t)=0$.
-
Montrer qu'il est possible d'écrire à la main une solution exacte de $f(t)=0$ à l'aide d'une des fonctions vues dans ce chapitre.
-
En déduire à la main toutes les solutions exacte de l'équation $f(t)=0$ sur l'intervalle $[0;1]$.
-
Trouver toutes ces solutions sur Xcas.
Les moments où le marteau est immobile par rapport à l'enclume correspondent aux instants $t$ tels que $f(t)=0$.
Courbe représentative de la fonction $\arctan$
-
Tracer sur Geogebra la fonction $\tan$ réduite à l'intervalle $\left]-\dfrac{\pi}{2};\dfrac{\pi}{2}\right[$ ainsi que la fonction $\arctan$.
Pour réduire le tracé d'une fonction
f(t)à un intervalle[min;max], il suffit de saisir :Fonction[f(t),min,max]. -
Que remarquez-vous quant aux deux courbes d'un point de vue symétrie ?
Les courbes représentant la fonction $\arctan$ et la fonction tangente réduite à l'intervalle $\left]-\dfrac{\pi}{2};\dfrac{\pi}{2}\right[$
sont symétriques par rapport à la droite d'équation $y=x$.
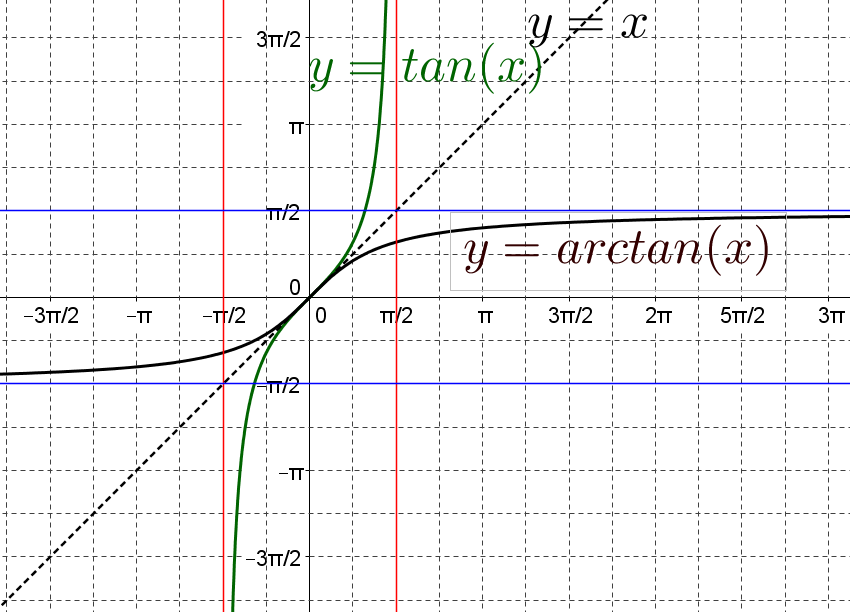
Cette propriété de symétrie entre les courbes représentant deux fonctions réciproques l'une de l'autre est vraie plus généralement. On l'observe déjà pour :
-
La fonction carrée réduite à l'intervalle $[0;+\infty[$ et la fonction racine carrée :
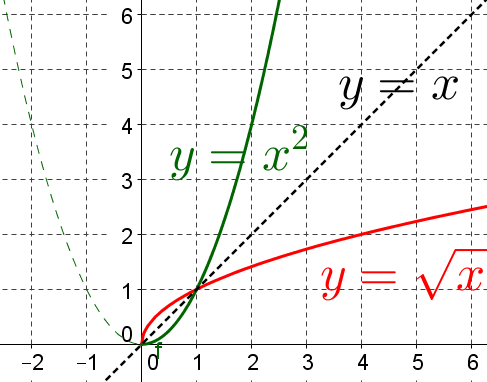 .
.
-
La fonction exponentielle et la fonction logarithme népérien :
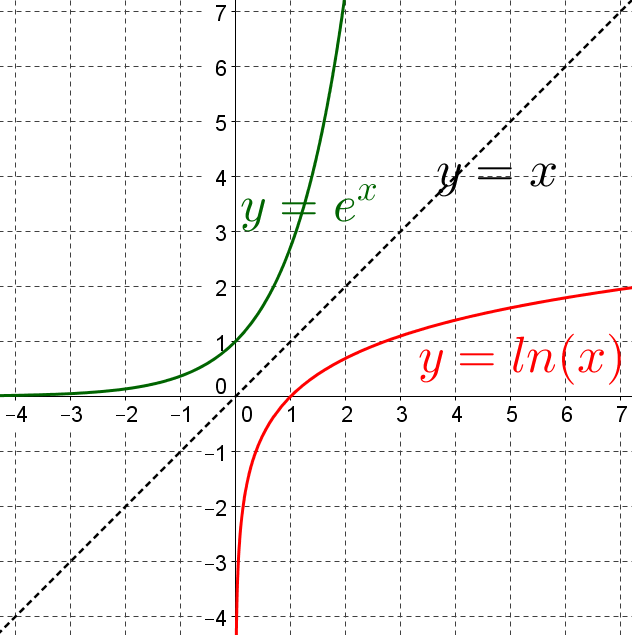 .
.
-
Comme $\displaystyle\lim_{t\to +\infty}\arctan(t)=\dfrac{\pi}{2}$, la courbe représentant la fonction $\arctan$ admet une asymptote horizontale d’équation $y=\dfrac{\pi}{2}$ au voisinage de $+\infty$.
-
Comme $\displaystyle\lim_{t\to -\infty}\arctan(t)=-\dfrac{\pi}{2}$, la courbe représentant la fonction $\arctan$ admet une asymptote horizontale d’équation $y=-\dfrac{\pi}{2}$ au voisinage de $-\infty$.
Dérivée de la fonction $\arctan$
-
La fonction arctangente est dérivable sur $\mathbb{R}$ avec pour tout réel $t$ : $(\arctan(t))'=\dfrac{1}{1+t^2}$.
-
Quelle que soit la fonction $u$ dérivable sur $\mathbb{R}$, on a : $(\arctan(u))'=\dfrac{u'}{1+u^2}$.
-
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(t)=\arctan(t^2)$.
Calculer (à la main si possible) $f'(t)$. -
Soit $g$ la fonction définie sur $\mathbb{R}$ par $g(t)=\arctan\left(\dfrac{1-t^2}{1+t^2}\right)$.
Calculer sur Xcas la forme simplifiée de $g'(t)$. -
On considère la fonction $s$ définie sur $\mathbb{R}$ par $s(t)=f(t)+g(t)$.
Justifier que pour tout réel $t$ : $s'(t)=0$. -
Calculer $s(0)$.
-
En déduire que pour tout réel $t$, $s(t)=\dfrac{\pi}{4}$.
-
En déduire que pour tout réel $t$, $\arctan\left(\dfrac{1-t^2}{1+t^2}\right)=\dfrac{\pi}{4}-\arctan(t^2)$.
-
En déduire en remplaçant $t$ par $\dfrac{1}{\sqrt{2}}$, montrer qu'il existe deux entiers $m$ et $n$ tels que $\dfrac{\pi}{4}=\arctan\left(\dfrac{1}{m}\right)+\arctan\left(\dfrac{1}{n}\right)$.
Cette égalité a été trouvée (d'une autre manière) et publiée par Euler en 1737 mais déjà connue par Machin en 1706.
Machin a utilisée une formule proche, $16\arctan\left(\dfrac{1}{5}\right)-4\arctan\left(\dfrac{1}{239}\right)=\pi$, pour calculer à la main les 100 premières décimales du nombre $\pi$ : un record pour l'époque !
Ce type de formule a été utilisée pour obtenir les premières décimales de $\pi$.
Par exemple, en 2002, le record de décimales connues de $\pi$ fut battu pour atteindre 1241,1 milliards. L'outil informatique et les deux égalités suivantes furent utilisées :-
$\displaystyle {\frac {\pi }{4}}=12\arctan {\frac {1}{49}}+32\arctan {\frac {1}{57}}-5\arctan {\frac {1}{239}}+12\arctan {\frac {1}{110443}}$
-
$\displaystyle {\frac {\pi }{4}}=44\arctan {\frac {1}{57}}+7\arctan {\frac {1}{239}}-12\arctan {\frac {1}{682}}+24\arctan {\frac {1}{12943}}$
-
Le circuit ci-contre a une transmittance isochrone dont l'argument est défini pour toute pulsation
$\omega$ par $\phi(\omega)=-\arctan(RC\omega)$, avec $R>0$ et $C>0$.
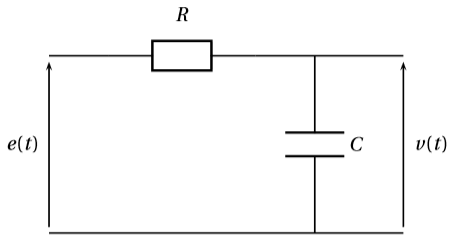
Déterminer comment évolue cet argument lorsque le pulsation augmente sur l'intervalle $]0;+\infty[$.
Exercices
Cercle trigonométrique
Résoudre les équations suivantes (à la main si possible) dans l'intervalle $[-\pi;\pi]$ :
-
$\cos(t)=-\dfrac{\sqrt{2}}{2}$.
-
$2\sin(t)-1=0$.
-
$\sin(t)=-\dfrac{\sqrt{3}}{2}$.
-
$3\sin(t)=6$.
-
$(2\sin(t)+\sqrt{3})(\cos(t)+1)=0$.
-
$-\dfrac{1}{2}\cos(t)=0$.
-
$2\cos(t)+4=0$.
-
-
Calculer $\sin(0)$, puis $\sin(\pi)$, $\sin(2\pi)$, $\sin(3\pi)$, ...
-
Simplifier $\sin(n\pi)$ avec $n$ un nombre entier.
-
-
-
Calculer $\cos(0)$, puis $\cos(\pi)$, $\cos(2\pi)$, $\cos(3\pi)$, ...
-
Simplifier $\cos(n\pi)$ avec $n$ un nombre entier.
-
Étude de fonctions trigonométriques
On décide de mettre en place un système de collecte des eaux de pluie sur
la façade d'une maison. Sur cette façade, de forme rectangulaire, deux tuyaux obliques doivent
récupérer l'eau de pluie pour la déverser dans un troisième tuyau vertical aboutissant à un réservoir.
On donne ci-dessous le plan de cette façade $ABCD$, dont les dimensions sont exprimées en mètres. Les deux premiers
tuyaux sont représentés par $[AM]$ et $[BM]$, le troisième tuyau par $[MH]$. $H$ est le milieu du segment $[DC]$.
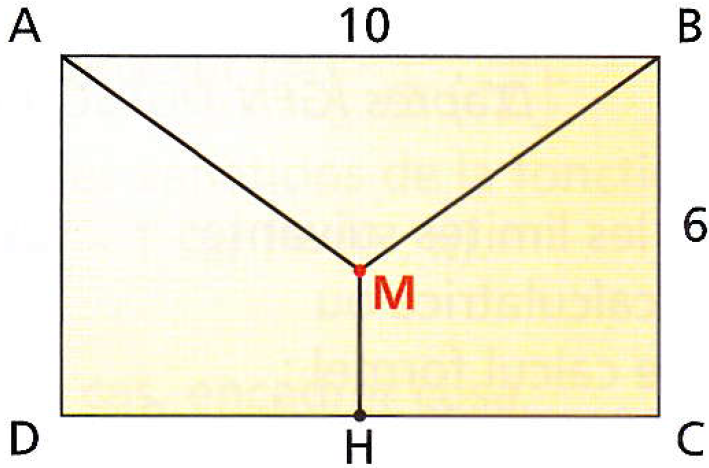
On souhaite trouver la position du point $M$ sur la façade qui permet de minimiser la longueur des tuyaux à acheter et donc la dépense à effectuer. On note $\theta$ l'angle $\widehat{BAM}$.
-
Calculer la longueur $MA$ en fonction de $\theta$.
Travailler dans le triangle $AMN$ où $N$ est le milieu du segment $[AB]$.
-
Justifier que $MH=6-5\tan(\theta)$.
-
En déduire que $MA+MB+MH=6+\dfrac{10-5\sin(\theta)}{\cos(\theta)}$.
-
Déterminer la valeur de $\theta$ qui minimise la longueur des tuyaux ainsi que la longueur nécessaire de ces tuyaux.
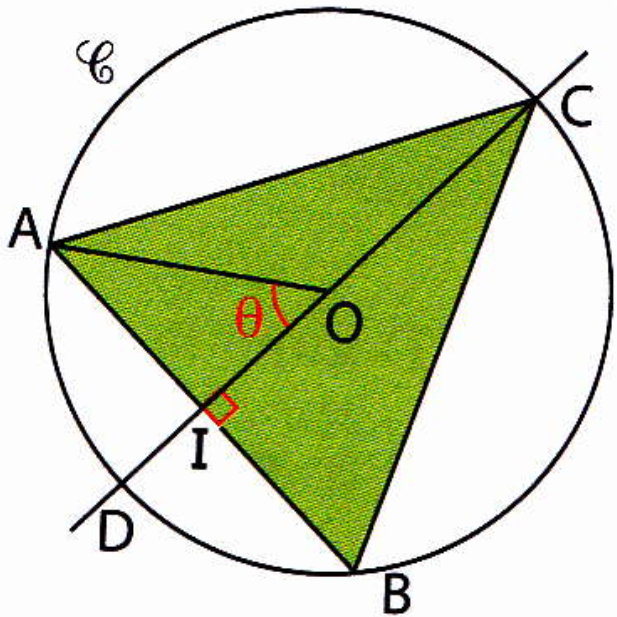
$\mathcal{C}$ est un cercle de centre $O$ et de rayon $r$.
$[CD]$ est un diamètre de $\mathcal{C}$ et $A$ est un point de $\mathcal{C}$ tel que $\widehat{AOD}=\theta$ avec
$\theta \in ]0;\pi[$.
$B$ est le point de $\mathcal{C}$ tel que la corde $[AB]$ est perpendiculaire à $(CD)$ en un point $I$.
-
Exprimer les longueurs $AI$ et $OI$ en fonction de l'angle $\theta$ et de la longueur $r$.
-
En déduire que l'aire $S(\theta)$ du triangle $ACB$ est donné par $S(\theta)=r^2(1+\cos(\theta))\times \sin(\theta)$.
-
On admet que l'on peut écrire la dérivée de $S$ sous la forme $S'(\theta)=r^2(\cos(\theta)+1)(2\cos(\theta)-1)$.
Déterminer l'angle $\theta$ qui permet de maximiser l'aire $S(\theta)$. -
Quelle est la nature du triangle $ACB$ d'aire maximale ? Exprimer cette aire en fonction de $r$.
Fonction $\arctan$
Soit $f$ la fonction définie sur $]-\infty;0[\cup ]0;+\infty[$ par $f(t)=\arctan(t)+\arctan\left(\dfrac{1}{t}\right)$.
-
-
Calculer, à la main si possible, $\displaystyle \left( \arctan\left(\dfrac{1}{t}\right)\right)^{'}$.
-
En déduire l'expression simplifiée de $f'(t)$.
-
Qu'en déduire pour la fonction $f$ ?
-
-
-
Calculer $f(1)$.
-
En déduire une égalité liant $\arctan(t)$ et $\arctan\left(\dfrac{1}{t}\right)$, lorsque $t>0$.
-
Vérifier cette égalité sur Xcas.
-
Soit $f$ la fonction définie sur l'intervalle $]1;+\infty[$ par $f(t)=\arctan\left(\dfrac{t}{t+1}\right)+\arctan\left(\dfrac{t}{t-1}\right)+\arctan(2 t^2)$.
-
-
Calculer, à la main si possible, la dérivée de $t\mapsto \arctan(2 t^2)$.
-
Déterminer, à l'aide de Xcas, sur l'intervalle $]1;+\infty[$, l'expression de $f'(t)$.
-
Qu'en déduire pour $f$ ?
-
-
-
Calculer la limite suivante : $\displaystyle \lim_{t\to +\infty} \arctan(2 t^2)$.
-
Calculer la limite suivante : $\displaystyle \lim_{t\to +\infty} \arctan\left(\dfrac{t}{t+1}\right)$.
-
Calculer la limite suivante : $\displaystyle \lim_{t\to +\infty} \arctan\left(\dfrac{t}{t-1}\right)$.
-
En déduire que pour réel $t\gt 1$, on a : $\arctan\left(\dfrac{t}{t+1}\right)+\arctan\left(\dfrac{t}{t-1}\right)+\arctan(2 t^2)=\pi$.
-
Justifier que $\arctan\left(\dfrac{2}{3}\right)+\arctan\left(2\right)+\arctan(8)=\pi$.
-
Un filtre à avance de phase a une fonction de transfert isochrone dont un argument est donné par la fonction suivante : $\theta(\omega)=\arctan\left(\dfrac{3\omega}{4+\omega ^2}\right)$ avec $\omega \in [0;+\infty[$.
-
Calculer $\theta(0)$.
-
Calculer la limite lorsque $\omega$ tend vers $+\infty$ de $\theta(\omega)$.
-
Dresser le tableau de variation complet (c'est-à-dire avec les limites) de $\theta$ sur $[0;+\infty[$.
-
En déduire la valeur de $\omega$ qui maximise l’argument $\theta(\omega)$ et donner la valeur maximale de $\theta$.
Partie A
Soit $f$ la fonction représentée par la courbe ci-contre $\mathcal{C}_f$ :
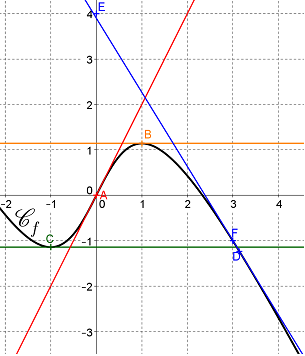
Plusieurs de ses tangentes sont aussi tracées.
-
Lire graphiquement $f'(0)$, $f'(1)$ et $f'(-1)$.
-
La tangente au point d'abscisse $\pi$ est très proche de la droite $(EF)$.
En déduire, par lecture graphique, une valeur approchée de $f'(\pi)$.
Partie B
La fonction $f$ est définie sur $\mathbb{R}$ par $f(t)=4\arctan(t)-2t$.
-
Vérifier que pour tout réel $t$, on a : $f'(t)=\dfrac{2(1-t^2)}{1+t^2}$.
-
Retrouver par calcul les valeurs exactes de $f'(0)$, $f'(1)$ et $f'(-1)$ puis celle exacte et approchée de $f'(\pi)$.
Le circuit ci-dessous est alimenté par un courant alternatif de pulsation $\omega$ avec $\omega \in [0;+\infty[$.
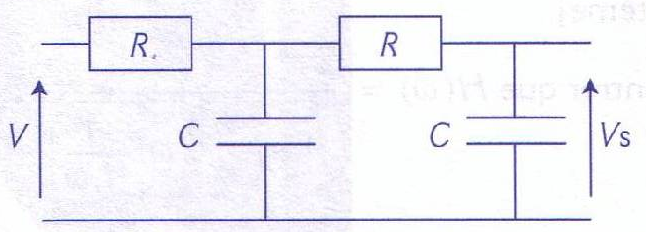
On admet que la fonction de transfert en tension a pour argument $\phi(\omega)=\arctan\left(\dfrac{RC}{(RC\omega)^2-1}\right)$.
On pose $K=RC$. On étudie ainsi la fonction $f$ définie par $f(t)=\arctan\left(\dfrac{K}{(K t)^2-1}\right)$
-
Justifier que la fonction $f$ est paire.
-
Déterminer la limite de $f$ lorsque $t$ tend vers $+\infty$.
-
Que se passe-t-il lorsque $t$ se rapproche de la valeur $\dfrac{1}{K}$ ? (Deux cas à différencier).
-
Déterminer l'expression de la dérivée $f'(t)$
-
Dresser le tableau de variations complet de $f$ sur $[0;+\infty[$ en précisant les limites et la valeur interdite.
Dans toute la suite, on travaille avec $t\ge 0$ tel que $f(t)$ existe.
Demander le programme !
-
Savoir ce qu'est le cercle trigonométrique.
-
Savoir les valeurs remarquables du cercle trigonométrique.
-
Savoir la définition d'une fonction paire, d'une fonction impaire.
-
Savoir la définition d'une fonction périodique de période $k$.
-
Savoir qu'il peut exister une infinité de fonctions solutions à une équation différentielle du premier ordre donnée.
-
Savoir que rajouter une condition particulière à une équation différentielle conduit à l'unicité de la fonction solution cherchée.
-
Savoir les formules de dérivation des différentes fonctions trigonométriques au programme.
-
Savoir la définition de la fonction tangente.
-
Savoir la définition de la fonction arctangente.
-
Savoir l'allure de la courbe représentative de chaque fonction trigonométrique au programme.
-
Savoir résoudre à la main des équations trigonométriques simples en s'appuyant sur le cercle trigonométrique.
-
Savoir résoudre sur Xcas une équation trigonométrique.
-
Savoir utiliser sur Xcas les instructions
supposonsetpurgepour résoudre des équations en réduisant l'intervalle d'étude ou en imposant des conditions sur des paramètres. -
Savoir modéliser des problèmes concrets.
-
Savoir reconnaître graphiquement une fonction paire, une fonction impaire, une fonction périodique.
-
Savoir tracer la représentation graphique d'une fonction présentant une propriété de parité ou de périodicité.
-
Savoir étudier à la main les variations d'une fonction trigonométrique simple.
-
Savoir étudier à l'aide de Xcas les variations d'une fonction trigonométrique quelconque.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International